ЗНО по математике: интеграл и метод интервалов

Задача 27. Интеграл
Вычислите $\int\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}}{5 ctg x \sin x dx}$

Решение
Преобразуем подынтегральное выражение

$ctg x \sin x = \frac{\cos x}{\sin x}\sin x=\cos x$
Таким образом, интеграл примет вид:

$\int\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}}{5 \cos x dx}=5\sin x | _{\frac{\pi}{6}}^{\frac{\pi}{2}}=5\left(\sin \frac{\pi}{2} - \sin \frac{\pi}{6}\right)=5\left(1-\frac{1}{2}\right) = 2,5$

Ответ: 2,5

Чтобы решить эту задачу, нужно  знать:

• Связь между тригонометрическими функциями
• Таблицу первообразных
• Значения синусов табличных углов.

Задача 28. Решение неравенства
Решите неравенство $(18+2x)^2(x^2+8x+15)\leq 0$. В ответ запишите сумму всех целых решений.

Решение

Рассмотрим множители по отдельности.
$(18+2x)^2\geq 0$ всегда. Равенство достигается при x=-9

Квадратный трёхчлен $x^2+8x+15$ раскладывается на множители как (x+3)(x+5). Нулю он равняется при х = -3 или х = -5.

Итак, имеем 3 корня, два - первой кратности и один - второй.

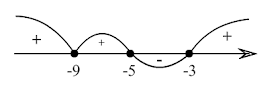
Отобразим все корни на числовой прямой. Так как неравенство нестрогое, ксе точки закрашиваются.

Возьмём какое-либо значение х за правым корнем. Удобно брать х = 0. Если подставить 0 в неравенство, получим значение $18^2\cdot 15 >0$. Начинаем строить "змейку", учитывая, что в корнях нечётной кратности она будет менять знак, а в корнях чётной - не будет.

Вот, что должно получиться:

Решением неравенства будет множество: $x\in \left{-9\right}\cup [-5;-3]$

Целые значения, удовлетворяющие условию, это: -9, -5, -4, -3. Их сумма составит -21. Именно это число и нужно записать в ответ.

Ответ: -21