На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии. Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.
А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.
Будем опираться на следующие формулы:
Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:
А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.
Будем опираться на следующие формулы:
- Основное тригонометрическое тождество: sin2a+cos2a = 1
- Определение тангенса:
- Определение котангенса:
- Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
- Формула косинуса суммы: cos(a+b) = cosacosb-sinasinb
Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:
- Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb-cosasinb
- Косинус разности: cos(a-b) = cosacos(-b)-sinasin(-b) = cosacosb+sinasinb
- Синус двойного угла: sin2a = sin(a+a) = sinacosa+cosasina = 2sinacosa
- Косинус двойного угла: cos2a = cos(a+a) = cosacosa-sinasina = cos2a-sin2a
- Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos2a-sin2a)sina = 2sinacos2a+sinacos2a-sin3a = 3sinacos2a-sin3a = 3sina(1-sin2a)-sin3a = 3sina-4sin3a
- Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa-sin2asina = (cos2a-sin2a)cosa-(2sinacosa)sina = cos3a-sin2acosa-2sin2acosa = cos3a-3sin2acosa = cos3a-3(1-cos2a)cosa = 4cos3a-3cosa
Прежде чем двигаться дальше, рассмотрим одну задачу.
Дано: угол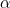 - острый.
- острый.
Найти его косинус, если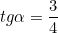
Решение, данное одним учеником:
Т.к.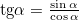 , то sina = 3,а cosa = 4.
, то sina = 3,а cosa = 4.
(Из математического юмора)
Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin2a+cos2a = 1 и разделим его на cos2a. Получим:
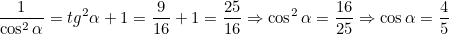
(Т.к. угол острый, при извлечении корня берётся знак +)
cos2a = cos2a-sin2a
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos2a+1 = cos2a-sin2a+cos2a+sin2a
2cos2a = cos2a+1
Выражая cosa через cos2a и выполняя замену переменных, получаем:
Аналогично, отняв от левой части равенства единицу, а от правой - сумму квадратов синуса и косинуса, получим:
cos2a-1 = cos2a-sin2a-cos2a-sin2a
2sin2a = 1-cos2a
sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.
Поскольку a = x+y, b = x-y, то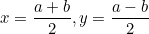 . Поэтому
. Поэтому
Дано: угол
Найти его косинус, если
Решение, данное одним учеником:
Т.к.
(Из математического юмора)
Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin2a+cos2a = 1 и разделим его на cos2a. Получим:
- Связь тангенса и косинуса:
(Т.к. угол острый, при извлечении корня берётся знак +)
- Аналогично получаем связь котангенса и синуса:
- Формула тангенса суммы:
. Разделив числитель и знаменатель на произведение косинусов, получим:
- Формула тангенса двойного угла:
cos2a = cos2a-sin2a
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos2a+1 = cos2a-sin2a+cos2a+sin2a
2cos2a = cos2a+1
Выражая cosa через cos2a и выполняя замену переменных, получаем:
- Косинус половинного угла:
Аналогично, отняв от левой части равенства единицу, а от правой - сумму квадратов синуса и косинуса, получим:
cos2a-1 = cos2a-sin2a-cos2a-sin2a
2sin2a = 1-cos2a
- Cинус половинного угла:
sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.
Поскольку a = x+y, b = x-y, то
- Представление суммы синусов в виде произведения:
- Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))
мне непонятен переход 3sina(1-sin2a)-sin3a = 3sina-4sin3a
ОтветитьУдалить