Приглашение в мир математики: Как находить бесконечные суммы: часть 2

В первой части мы нашли суммы следующих рядов:
$\frac{1}{1} + \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \frac{1}{2^4} + \dots=2$
$\frac{1}{2} + \frac{1}{6} + \frac{1}{3\cdot 4} + \frac{1}{4\cdot 5} + \frac{1}{5\cdot 6} + \dots=1$
$\frac{1}{1} + \frac{2}{2} + \frac{3}{2^2} + \frac{4}{2^3} + \frac{5}{2^4} + \dots=4$ .

Рассмотрим теперь, что будет, если в третьем ряду числители будут образовывать не арифметическую прогрессию, а последовательность Фибоначчи. Найдём сумму:

$S=\frac{1}{1} + \frac{1}{2} + \frac{2}{2^2} + \frac{3}{2^3} + \frac{5}{2^4} + \frac{8}{2^5} + \frac{13}{2^6} + \dots$ .

Опять-таки применим метод деления и найдём, чему равна половина этой суммы:

$\frac{S}{2}=\frac{1}{2} + \frac{1}{2^2} + \frac{2}{2^3} + \frac{3}{2^4} + \frac{5}{2^5} + \frac{8}{2^6} + \frac{13}{2^7} + \dots$ .

Bычтем из первого равенства второе:

$S-\frac{S}{2}=\frac{1}{1} + \frac{1-1}{2} + \frac{2-1}{2^2} + \frac{3-2}{2^3} + \frac{5-3}{2^4} + \frac{8-5}{2^5} + \frac{13-8}{2^6} + \dots$

$\frac{S}{2}=1 + \frac{1}{2^2} + \frac{1}{2^3} + \frac{2}{2^4} + \frac{3}{2^5} + \frac{5}{2^6} + \dots$

Но ведь справа после первой единицы идёт исходная последовательность, разделённая на 4, поэтому:

$\frac{S}{2}=1 + \frac{S}{4}$

Значит, S=4.

Итак,
$\frac{1}{1} + \frac{1}{2} + \frac{2}{2^2} + \frac{3}{2^3} + \frac{5}{2^4} + \frac{8}{2^5} + \frac{13}{2^6} + \dots=4$ .

А вот ещё один интересный способ решения таких задач, который был применён Эйлером для нахождения суммы обратных квадратов:

$\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \dots$ .

Сделаем сначала небольшое отступление. Всем известно, что многочлен n-й степени с корнями x₁,x₂,…x_n может быть представлен в виде произведения A(x₁-x)(x₂-x)…(x_n-x). При этом значение многочлена в точке x=0 будет равно Ax₁x₂…x_n. Если мы хотим, чтобы это значение было равно единице, коэффициент A следует взять равным
$A=\frac{1}{x_1\cdot x_2\cdot \dots \cdot x_n}$

Тогда данный многочлен может быть записан как:
$\frac{(x_1-x)(x_2-x)\dots(x_n-x)}{x_1\cdot x_2\cdot \dots \cdot x_n}=\frac{x_1-x}{x_1}\cdot\frac{x_2-x}{x_2}\cdot \dots\cdot \frac{x_n-x}{x_n}=$
$=\left(1-\frac{x}{x_1}\right) \left(1-\frac{x}{x_2}\right)\dots \left(1-\frac{x}{x_n}\right)$

Возьмём функцию $\frac{\sin x}{x}$ . Хотя её значение в точке x=0 не существует, но в окрестностях её будет стремиться к единице. Кроме того, ось Ox график этой функции будет пересекать в точках $\pi n,~n \in Z,~n\neq0$ . Так что можно представить её следующим бесконечным произведением

$img=yh2z7o2$

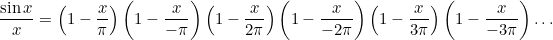
Соседние множители можно объединить по формуле разности квадратов:

$\frac{\sin x}{x}=\left(1-\frac{x^2}{\pi^2}\right) \left(1-\frac{x^}{4\pi^2}\right) \left(1-\frac{x^2}{9\pi^2}\right) \dots$

С другой стороны, поскольку функция синус раскладывается в ряд Маклорена следующим образом:
$\sin x=x-\frac{x^3}{3!}-\frac{x^5}{5!}-\frac{x^7}{7!} + \dots$

то
$\frac{\sin x}{x}=1-\frac{x^2}{3!}-\frac{x^4}{5!}-\frac{x^6}{7!} + \dots$

Этот многочлен и получившийся в результате перемножения бесконечного произведения должны быть тождественно равны.

Свободные члены и там, и там равны единице. А при квадрате икса в ряду Маклорена стоит коэффициент $-\frac{1}{6}$ , а в ряду, полученном из произведения, при x² будет стоять сумма $-\left(\frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \dots\right)$ .

Значит
$\frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \dots=\frac{1}{6}$

Домножив обе части на квадрат пи, получим:
$\frac{1}{1} + \frac{1}{4} + \frac{1}{9} + \dots=\frac{\pi^2}{6}$

Итак, и эта сумма найдена.

Увидев столько интересных сумм задумываешься: а что получится, если просто складывать дроби
$\frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \dots$

Может, тут тоже сумма будет равна какому-нибудь целому числу или будет выражаться формулой, куда входят пи или е?

Оказывается, нет. Эта сумма будет расти до бесконечности, и сейчас мы докажем это.
Для этого рассмотрим следующие соотношения:

1 = 1
$\frac{1}{2}=\frac{1}{2}$
$\frac{1}{3} + \frac{1}{4}>\frac{2}{4} =\frac{1}{2}$
$\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8}>\frac{4}{8} =\frac{1}{2}$
$\frac{1}{9} + \frac{1}{10} + \frac{1}{11} + \frac{1}{12} + \frac{1}{13} + \frac{1}{14} + \frac{1}{15} + \frac{1}{16}>\frac{8}{16} =\frac{1}{2}$
…

Видите? Сумма 2ⁿ слагаемых больше, чем $1 + \frac{n}{2}$ , и следующие 2ⁿ слагаемых увеличивают эту сумму ещё на величину, большую, чем $\frac{1}{2}$ . Так что суммируя обратные величины натурального ряда (такой ряд ещё называется гармоническим), можно превысить любое наперёд заданное число. По-другому можно сказать, что это ряд расходится.

На этом свойстве гармонического ряда основано много красивых задач. Но это уже совсем другая история :)

Pages

Как находить бесконечные суммы: часть 2