Приглашение в мир математики: Решение задачи 3. Сумма ряда

Условие задачи

Найдите закономерность и вычислите сумму всех элементов последовательности
$img=yax4urf$

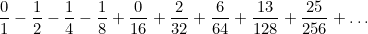
Решение

Сначала найдём закономерность. Понятно, что знаменатели представляют собой последовательные степени двойки.

Рассмотрим последовательность числителей и вычислим разности первого и второго порядка:
0, -1, -1, -1, 0, 2, 6, 13, 25
-1, 0. 0. 1, 2, 4, 7, 12
1, 0, 1, 1, 2, 3, 5

Можно заметить, что разности второго порядка – это последовательность Фибоначчи!

Попробуем обнаружить некий рекуррентный закон среди разностей первого порядка.
-1, 0. 0. 1, 2, 4, 7, 12 - Здесь каждый последующий член на единицу больше суммы двух предыдущих. Это позволяет найти закономерность в исходной последовательности:
0, -1, -1, -1, 0, 2, 6, 13, 25 - $a_{n + 2}=a_{n + 1} + a_n + n-1$ ,если начинать с индекса, равного 1

Можно для неё вывести формулу общего члена и таким образом свернуть ряд, но можно заметить, что последовательность
0, -1, -1, -1, 0, 2, 6, 13, 25, …
представляет собой разность последовательностей Фибоначчи
1, 1, 2, 3, 5, 8, 13, 21, 34
и натурального ряда
1, 2, 3, 4, 5, 6, 7, 8, 9

Так что искомая сумма равна
$\frac{1-1}{1} + \frac{1-2}{2} + \frac{2-3}{2^2} + \frac{3-4}{2^3} + \frac{5-5}{2^4} + \frac{8-6}{2^5} + \frac{13-7}{2^6} + \frac{13-8}{2^6} + \frac{13-9}{2^6} + \dots=$ $\left(\frac{1}{1} + \frac{1}{2} + \frac{2}{2^2} + \frac{3}{2^3} + \frac{5}{2^4} + \frac{8}{2^5} + \frac{13}{2^6} + \dots\right)$ $-\left(\frac{1}{1} + \frac{2}{2} + \frac{3}{2^2} + \frac{4}{2^3} + \frac{5}{2^4} + \dots \right)=4-4=0$
Подробнее о том, как вычисляются эти суммы можно почитать в статье о суммировании бесконечных рядов.

<К условиям задач олимпиады

Pages

Решение задачи 3. Сумма ряда