Вторая открытая Интернет-олимпиада по математике проводилась в мае 2010 года. Для решения предлагалось 7 нестандартных задач, оценивающихся по 7 баллов каждая.Принять участие могли все желающие.
Задача 1. Приближение произведением
Отношение двух наименьших трёхзначных простых чисел равно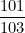 =0,980583…
=0,980583…
Найдите несколько таких простых дробей с числителями и знаменателями, не превосходящими 50, произведение которых отличалось бы от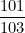 менее чем на 10-5
менее чем на 10-5
Решение задачи
Задача 2. Стохастический Баше
Вася и Петя отлично умеют анализировать Баше-подобные игры, поэтому они решили несколько разнообразить игровой процесс.
Сначала Вася называет некоторое число 50<N<100. На стол кладётся N спичек.
Далее при помощи обычного игрального кубика (с числами от 1 до 6 на гранях) выбрасываются три числа: a, b и c (2 или 3 из них могут оказаться равными).
Игроки по очереди берут из стопки a, b или c спичек. Проигрывает тот, кто не может сделать ход.
Какое число нужно назвать Васе, чтобы максимизировать свои шансы на выигрыш, если первым будет ходить Петя?
Решение задачи
Задача 3. Сумма ряда
Найдите закономерность и вычислите сумму всех элементов последовательности
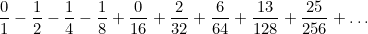
Решение задачи
Задача 4. Карты
На столе в закрытую лежат 8 карт. Известно, что там 4 красные и 4 чёрные карты. Вы выбираете из них две случайным образом. Какова вероятность того, что эти две карты окажутся одного цвета?
Решение задачи
Задача 5. Треугольник из отрезков
Единичный отрезок случайным образом разбивается на две части. Затем большая часть опять случайным образом разбивается на две. Какова вероятность того, что из этих трёх частей можно составить треугольник?
Решение задачи
Задача 6. Больше всего сумм
Найдите четырёхзначное число, которое можно представить в виде суммы нескольких последовательных натуральных чисел наибольшим количеством способов.
Решение задачи
Задача 7. Жук на ленте
Один конец резиновой ленты неподвижно закреплён, а за другой тянут с постоянной скоростью v. У неподвижного конца ленты находится жук, который начинает ползти вдоль неё со скоростью u. Когда жук доползёт до противоположного конца ленты, если начальная длина ленты равна L?
Решение задачи
Задача 1. Приближение произведением
Отношение двух наименьших трёхзначных простых чисел равно
Найдите несколько таких простых дробей с числителями и знаменателями, не превосходящими 50, произведение которых отличалось бы от
Решение задачи
Задача 2. Стохастический Баше
Вася и Петя отлично умеют анализировать Баше-подобные игры, поэтому они решили несколько разнообразить игровой процесс.
Сначала Вася называет некоторое число 50<N<100. На стол кладётся N спичек.
Далее при помощи обычного игрального кубика (с числами от 1 до 6 на гранях) выбрасываются три числа: a, b и c (2 или 3 из них могут оказаться равными).
Игроки по очереди берут из стопки a, b или c спичек. Проигрывает тот, кто не может сделать ход.
Какое число нужно назвать Васе, чтобы максимизировать свои шансы на выигрыш, если первым будет ходить Петя?
Решение задачи
Задача 3. Сумма ряда
Найдите закономерность и вычислите сумму всех элементов последовательности
Решение задачи
Задача 4. Карты
На столе в закрытую лежат 8 карт. Известно, что там 4 красные и 4 чёрные карты. Вы выбираете из них две случайным образом. Какова вероятность того, что эти две карты окажутся одного цвета?
Решение задачи
Задача 5. Треугольник из отрезков
Единичный отрезок случайным образом разбивается на две части. Затем большая часть опять случайным образом разбивается на две. Какова вероятность того, что из этих трёх частей можно составить треугольник?
Решение задачи
Задача 6. Больше всего сумм
Найдите четырёхзначное число, которое можно представить в виде суммы нескольких последовательных натуральных чисел наибольшим количеством способов.
Решение задачи
Задача 7. Жук на ленте
Один конец резиновой ленты неподвижно закреплён, а за другой тянут с постоянной скоростью v. У неподвижного конца ленты находится жук, который начинает ползти вдоль неё со скоростью u. Когда жук доползёт до противоположного конца ленты, если начальная длина ленты равна L?
Решение задачи