В первой части мы нашли суммы следующих рядов:


 .
.
Рассмотрим теперь, что будет, если в третьем ряду числители будут образовывать не арифметическую прогрессию, а последовательность Фибоначчи. Найдём сумму:
 .
.
Опять-таки применим метод деления и найдём, чему равна половина этой суммы:
 .
.
Bычтем из первого равенства второе:


Но ведь справа после первой единицы идёт исходная последовательность, разделённая на 4, поэтому:

Значит, S=4.
Итак,
 .
.
А вот ещё один интересный способ решения таких задач, который был применён Эйлером для нахождения суммы обратных квадратов:
 .
.
Сделаем сначала небольшое отступление. Всем известно, что многочлен n-й степени с корнями x1,x2,…xn может быть представлен в виде произведения A(x1-x)(x2-x)…(xn-x). При этом значение многочлена в точке x=0 будет равно Ax1x2…xn. Если мы хотим, чтобы это значение было равно единице, коэффициент A следует взять равным

Тогда данный многочлен может быть записан как:
(x_2-x)\dots(x_n-x)}{x_1\cdot x_2\cdot \dots \cdot x_n}=\frac{x_1-x}{x_1}\cdot\frac{x_2-x}{x_2}\cdot \dots\cdot \frac{x_n-x}{x_n}=)
 \left(1-\frac{x}{x_2}\right)\dots \left(1-\frac{x}{x_n}\right))
Возьмём функцию . Хотя её значение в точке x=0 не существует, но в окрестностях её будет стремиться к единице. Кроме того, ось Ox график этой функции будет пересекать в точках
. Хотя её значение в точке x=0 не существует, но в окрестностях её будет стремиться к единице. Кроме того, ось Ox график этой функции будет пересекать в точках  . Так что можно представить её следующим бесконечным произведением
. Так что можно представить её следующим бесконечным произведением
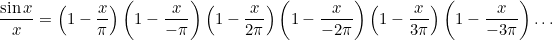
Соседние множители можно объединить по формуле разности квадратов:
 \left(1-\frac{x^}{4\pi^2}\right) \left(1-\frac{x^2}{9\pi^2}\right) \dots )
С другой стороны, поскольку функция синус раскладывается в ряд Маклорена следующим образом:

то

Этот многочлен и получившийся в результате перемножения бесконечного произведения должны быть тождественно равны.
Свободные члены и там, и там равны единице. А при квадрате икса в ряду Маклорена стоит коэффициент , а в ряду, полученном из произведения, при x2 будет стоять сумма
, а в ряду, полученном из произведения, при x2 будет стоять сумма ) .
.
Значит

Домножив обе части на квадрат пи, получим:

Итак, и эта сумма найдена.
Увидев столько интересных сумм задумываешься: а что получится, если просто складывать дроби

Может, тут тоже сумма будет равна какому-нибудь целому числу или будет выражаться формулой, куда входят пи или е?
Оказывается, нет. Эта сумма будет расти до бесконечности, и сейчас мы докажем это.
Для этого рассмотрим следующие соотношения:
1 = 1




…
Видите? Сумма 2n слагаемых больше, чем , и следующие 2n слагаемых увеличивают эту сумму ещё на величину, большую, чем
, и следующие 2n слагаемых увеличивают эту сумму ещё на величину, большую, чем  . Так что суммируя обратные величины натурального ряда (такой ряд ещё называется гармоническим), можно превысить любое наперёд заданное число. По-другому можно сказать, что это ряд расходится.
. Так что суммируя обратные величины натурального ряда (такой ряд ещё называется гармоническим), можно превысить любое наперёд заданное число. По-другому можно сказать, что это ряд расходится.
На этом свойстве гармонического ряда основано много красивых задач. Но это уже совсем другая история :)
Рассмотрим теперь, что будет, если в третьем ряду числители будут образовывать не арифметическую прогрессию, а последовательность Фибоначчи. Найдём сумму:
Опять-таки применим метод деления и найдём, чему равна половина этой суммы:
Bычтем из первого равенства второе:
Но ведь справа после первой единицы идёт исходная последовательность, разделённая на 4, поэтому:
Значит, S=4.
Итак,
А вот ещё один интересный способ решения таких задач, который был применён Эйлером для нахождения суммы обратных квадратов:
Сделаем сначала небольшое отступление. Всем известно, что многочлен n-й степени с корнями x1,x2,…xn может быть представлен в виде произведения A(x1-x)(x2-x)…(xn-x). При этом значение многочлена в точке x=0 будет равно Ax1x2…xn. Если мы хотим, чтобы это значение было равно единице, коэффициент A следует взять равным
Тогда данный многочлен может быть записан как:
Возьмём функцию
Соседние множители можно объединить по формуле разности квадратов:
С другой стороны, поскольку функция синус раскладывается в ряд Маклорена следующим образом:
то
Этот многочлен и получившийся в результате перемножения бесконечного произведения должны быть тождественно равны.
Свободные члены и там, и там равны единице. А при квадрате икса в ряду Маклорена стоит коэффициент
Значит
Домножив обе части на квадрат пи, получим:
Итак, и эта сумма найдена.
Увидев столько интересных сумм задумываешься: а что получится, если просто складывать дроби
Может, тут тоже сумма будет равна какому-нибудь целому числу или будет выражаться формулой, куда входят пи или е?
Оказывается, нет. Эта сумма будет расти до бесконечности, и сейчас мы докажем это.
Для этого рассмотрим следующие соотношения:
1 = 1
…
Видите? Сумма 2n слагаемых больше, чем
На этом свойстве гармонического ряда основано много красивых задач. Но это уже совсем другая история :)