Задача 7. Карточки с картинками (3 балла).
У Красунчика есть 5 карточек, вот они:
Есть карточки, на которых с одной стороны нарисован цветок, а с другой - собака. А есть такие, на которых с одной стороны нарисована кошка, а с другой - дерево. Сколько карточек с цветочками у Красунчика?
Варианты ответа:
А: 1; Б: 2; В: 3; Г: 4; Д: 5;
Решение
Из условия понятно, что на карточках рисунки с двух сторон. Нам надо определить, какие рисунки на тех сторонах, которые не видны. Так как "одна" и "другая" стороны карточки равноценны, то утверждения из условия работают в обе стороны. Выходит, на первой карточке под деревом нарисована кошка. На второй под собакой - цветок. На третьей под кошкой - дерево. На четвёртой карточке снова под собакой нарисован цветок. И на пятой под цветком нарисована собака. Выходит, всего карточек с цветками три: вторая, четвёртая и пятая.
Кстати, двусторонние карточки используются в одной классической задаче на математическую логику, о которой мы как-нибудь расскажем в разделе Занимательной математики.
Правильный ответ: В 3
Задача 8. Зонтик "Кенгуру" (3 балла).
На моём зонтике написано слово KANGAROO, как показано на рисунке. На каком из предложенных в ответах рисунков тоже изображён мой зонтик?Эта задача проходит через несколько классов и использовалась для мониторинга уровня учеников.
Варианты ответа:
А:
; Б: 
; В: 
; Г: 
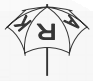; Д: 
;Решение
В условии зонтик мы видим сверху, а в ответах - сбоку. Так как слово KANGAROO написано по часовой стрелке, то при виде сбоку оно будет чисаться справа налево (и буквы будут перевёрнутыми). Вот почему эта задача выбрана для мониторинга в различных классах: никаких формул для решения она не требует, нужно только пространственное воображение.
Глядя на первый зонти видим последовательность NGA. Действительно, это часть слова KANGAROO. Это и дует правильным ответом. Можно убедиться, что ни GAN, ни KNG, ни ARK, ни RAG в надписи на зонтике не встретится.
Правильный ответ: А
Далее идут задачи посложнее, каждая оценивается в 4 балла
Задача 9. Разрезание фигуры (4 балла).
Хитрун разресал фигуру на рисунке на вот такие треугольники:
. Сколько треугольников у него получилось?
Варианты ответа:
А: 8; Б: 12; В: 14; Г: 15; Д: 16;
Решение
В этой задаче можно вспользоваться полезной уловкой. Так как среди вариантов ответа нет "это невозможно сделать", то такое разрезание возможно. А раз оно возможно, то достаточно площадь большой фигуры поделить на площадь маленького треугольничка.
Треугольник состоит из двух половинок клеток, значит, его площадь 1 квадратик. А площадь большой фигуры равна 15 квадратиков.
Можно и показать пример разрезания:
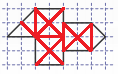
Правильный ответ: Г 15
Задача 10. Обмен фруктами (4 балла).
У Ласунчика 7 яблок и 2 банана. Он дал 2 яблока Соньку, а тот дал несколько бананов Ласунчику. Теперь у Ласунчика яблок и бананов стало поровну. Сколько бананов дал Сонько Ласунчику?
Варианты ответа:
А: 2; Б: 3; В: 4; Г: 5; Д: 7;
Решение
Решим задачу по вопросам.
Сколько яблок осталось у Ласунчика после того, как он отдал 2 яблока Соньку?
7-2 = 5 (яблок)
На сколько меньше у Лсунчика оказалось бананов, чем яблок?
5-2 = 3
Так как их стало поровну, то Ласунчик получил 3 банана.
Правильный ответ: Б 3
Задача 11. Куб из кубиков (4 балла).Веселун построил куб из 27 маленьких кубиков. Каждый кубик или белого или серого цвета. Кубики, у которых общая грань, разного цвета (как показано на рисунке). Сколько белых кубиков использовал Веселун?
Варианты ответа:
А: 10; Б: 12; В: 13; Г: 14; Д: 15;
Решение
Ещё одна задача на пространственное воображение. Верхний слой кубиков мы видим, он выглядит так:
А нижний слой будет таким же, как верхний:
Всего белых кубиков будет 4+5+4 = 13
Правильный ответ: В 13
Задача 12. Гонки на коньках (4 балла).
В соревнованиях по бегу на коньках 10 участников. Хитрун обогнал на 3 участников, чем обогнало его. Какое место занял Хитрун, если ни один из участников не пришёл к финишу одновременно с ним?
Варианты ответа:
А: 1-е; Б: 3-е; В: 4-е; Г: 6-е; Д: 7-е;
Решение
Кроме Хитруна было ещё 9 участников. Если условно убрать троих, которых Хитрун обогнал, то половина будет вперени него, половина - позади. Значит, из (9-3) = 6 участников половина, т.е. трое, обогнали Хитруна. А сам он, выходит, занял 4-е место, обогнав шестерых участников.
Правильный ответ: В 4-е
Комментариев нет :
Отправить комментарий