В 3 и 4 классах в задачах уже появляются элементы комбинаторики, математические ребусы, разрезания и классические рыцари и лжецы.
Задача 1. Цепочка вычислений (3 балла).
Какое число окажется в синем облачке, если все действия выполнить верно?
Варианты ответа:
А: 6; Б: 7; В: 8; Г: 10; Д: 15;
Решение
Выполним действия.
5-2 = 3
3-1 = 2
2х5 = 10
Значит, в синем облачке должно быть записано число 10.
Правильный ответ: Г 10
Задача 2. Конструктор (3 балла).
У Веселуна 10 одинаковых деталей конструктора.
С помощью гаек он собрал из них пять конструкций (показаны на рисунке). Какая конструкция оказалась самой короткой?
Варианты ответа:
А: A; Б: B; В: C; Г: D; Д: E;
Решение
Эта задача предлагалась и в олимпиаде для 2 класса. Там мы разобрали, как ребёнку её решать и не ошибиться.
Правильный ответ: Б Конструкция B
Задача 3. Числовой ребус (3 балла).
Какое число закрыто квадратом, если одинаковые числа закрыты одинаковыми фигурами?
Варианты ответа:
А: 2; Б: 3; В: 4; Г: 5; Д: 6;
Решение
Найдём, каое число закрыто треугольником. В первом выражении треугольник -это неизвестное слагаемое. Вспомним правило: "чтобы найти неизвестное слагаемое, нужно от суммы отнять известное слагаемое". Значит, число под треугольником равно 7-4 = 3.
Теперь второе выражение принимает вид:
квадратик + 3 = 9.
Квадратик в нём - неизвестное слагаемое. Находим его, отняв от суммы известное слагаемое.
квадратик = 9-3
квадратик = 6
Правильный ответ: Д 6
Задача 4. Девять точек на окружности (3 балла).
 Мудрагелик соединяет отрезками точки на окружности, не отрывая карандаша от бумаги. Он начинает с токи под номером 1 и соединяет точки через одну, пока снова не вернётся в точку номер 1. Первые два отрезка изображены на рисунке справа. Какое изображение получит в итоге Мудрагелик?
Мудрагелик соединяет отрезками точки на окружности, не отрывая карандаша от бумаги. Он начинает с токи под номером 1 и соединяет точки через одну, пока снова не вернётся в точку номер 1. Первые два отрезка изображены на рисунке справа. Какое изображение получит в итоге Мудрагелик?Варианты ответа:
А:
 ; Б:
; Б:  ; В:
; В:  ; Г:
; Г:  ; Д:
; Д:  ;
;Решение
Сделаем то же, что и делает кенгурёнок по имени Мудрагелик. После точки 5 мы попадём в точку 7. Из неё - в точку 9 (каждый раз мы соединяем точки через одну). Из точки 9, продолжая соединять точки через одну по часовой стрелке, мы попадём в точку 2. Из неё - в точку 4, затем - в точку 6 и в точку 8. А из точки 8 мы попадём в точку 1 и остановимся.
На каком из рисунков показан тот пусть, который получился у нас? Он показан на рисунке Д. Это и будет правильным ответом.
Правильный ответ: Д

Задача 5. Правильная тень (3 балла).
На каком из предложенных в ответах рисунков правильно нарисована тень от изгороди?
Варианты ответа:
А:
 ; Б:
; Б:  ; В:
; В: 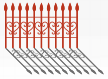 ; Г:
; Г:  ; Д:
; Д:  ;
;Решение
Ещё одна задача на внимательность к деталям. Рассмотрим внимательно заборы. Форма у них всех одинаковая, отличаются они только цветами. Заметим, что навершия у изгороди в виде пик, есть две горизонтальные перекладины, между которыми - узор, похожий на сердечки.
Какие несоответствия можно заметить в тенях?
В варианте А нет нижней горизонтальной перекладины,
В варианте Б нет пик,
В варианте В тоже нет нижней горизонтальной перекладины, а изображения сердечек сдвинуты ниже
Вариант Г похож на правильный
Окончательно убеждаемся в этом, увидев, что в варианте Д отсутствует тень у некоторых вертикальных частей.
Правильный ответ: Г

Задача 6. Двузначное число (3 балла).
Произведение цифр двузначного числа равно 15. Чему равна сумма цифр этого числа?
Варианты ответа:
А: 2; Б: 4; В: 6; Г: 7; Д: 8;
Решение
Вспомним таблицу умножения. Какие цифры, если их перемножить, дадут 15?
15 = 3х5 = 5х3. Значит, это число - 35 или 53. В любом случае, сумма его цифр будет равна 8.
(Конечно же, 15 можно получить ещё как 15 = 15х1 = 1х15, но нас интересует именно произведение цифр)
Правильный ответ: Д 8



Комментариев нет :
Отправить комментарий