 Первые 20 задач имеют по 5 вариантов ответа. Так что с вероятностью 0,2 на каждое из них будет дан правильный ответ, и математическое ожидание количества баллов угадывающего участника за первую часть теста равно 4.
Первые 20 задач имеют по 5 вариантов ответа. Так что с вероятностью 0,2 на каждое из них будет дан правильный ответ, и математическое ожидание количества баллов угадывающего участника за первую часть теста равно 4.Далее, вторая часть тестирования состоит из 4 задач, в каждой из которых четырём утверждениям из левого столбика (1-4) надо найти в соответствие одно из пяти утверждений в правом столбике (А-Д). За каждое правильно установленное соответствие начисляется по одному баллу.
Чему же равно математическое ожидание количества баллов угадывающего участника ЗНО за задачи второй части?
Решим для начала такую задачу. В скольких перестановках n элементов ровно k стоят на своих местах?
Обозначим искомое количество D(n,k).
Из n элементов можно выбрать k таких, которые будут стоять на своих местах $C_n^k$ способами. Эти k элементов устанавливаются однозначно. Остальные n-k элементов должны быть установлены так, чтобы не было ни одного совпадения номера элемента и номера места. Это можно сделать D(n-k,0) способами.
Получаем рекуррентную формулу:
$D(n,k)=C_n^k\cdot D(n-k,0)$
А количество способов переставить n элементов так, чтобы ни один не стоял на своём месте, равно $D(n,0)=n!-\sum\limits_{i=1}^n{D(n,i)}$
Также понятно, что D(n,n) = n!; D(n,n-1) = 0.
Теперь можно перейти к подсчётам:
Для одного элемента:
D(1,1) = 1; D(1,0) = 1!-1 = 0 - один элемент всегда попадёт на своё место.
Для двух элементов:
D(2,2) = 1; D(2,1) = 0; D(2,0) = 2!-0-1 = 1.
Для трёх элементов:
D(3,3) = 1; D(3,2) = 0; $D(3,1) = C_3^1\cdot D(2,0) = 3$; D(3,0) = 3!-3-1=2.
И для четырёх элементов:
D(4,4) = 1; D(4,3) = 0; $D(4,2) = C_4^2\cdot D(2,0) = 6\cdot 1 = 6$; $D(4,1) = C_4^1\cdot D(3,0) = 4\cdot 2 = 8$; D(4,0) = 4! - 8 - 6 - 1 = 9.
Итак, если бы на тестировании нужно было бы сопоставить 4 утверждения с четырьмя, то, из 24-х возможных вариантов, 9 принесли бы участнику 0 баллов, 8 - один балл, 6 - 2 балла, 0 - 3 балла и 1 - 4 балла.
Как изменится распределение, если допустить выбор пятого (абсолютно неправильного варианта)?
Рассмотрим перестановку n элементов по n местам такую, что ровно k из них стоят на своих местах. Тогда (n+1)-й элемент можно поставить на место одного из k элементов, стоящих на своих местах (и количество стоящих на своих местах элементов уменьшится на 1) или на место одного из (n-k) элементов, не стоящих на своих местах (что не повлияет на количество правильных соответствий). И стоит учесть также 1 случай, когда (n+1) элемент не заменяет ни одного из изначальных n.
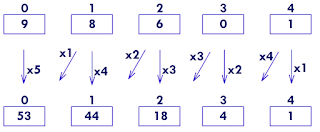
Всё это можно проиллюстрировать следующей схемой.
Получается, что вероятность расставить все ответы неправильно в задании второй части ЗНО равна $\frac{53}{120}\approx 0,44$, а математическое ожидание количества баллов за задачу равно
$1\cdot\frac{44}{120}+2\cdot\frac{18}{120}+3\cdot\frac{4}{120}+4\cdot\frac{1}{120} = 0,8$
Значит, математическое ожидание баллов за вторую часть ЗНО равно 3,2.
Итого, простым угадыванием можно набрать в среднем 7,2 балла.
Можно также определить, что вероятность не угадать ни одного верного варианта в тестировании равна $\left(\frac{4}{5}\right)^20\cdot\left(\frac{44}{120}\right)^4\approx 0,0002$, примерно две десятитысячных.
А вероятность набрать угадыванием 36 баллов, теоретический максимум для этого способа решения теста, составит $\left(\frac{1}{5}\right)^20\cdot\left(\frac{1}{120}\right)^4\approx 5\cdot 10^{-23}$. Это примерно в полтора квинтиллиона раз больше вероятности сорвать джекпот в лотерее "6 из 49".
Так что разбирайте задачи ЗНО прошлых лет - будет надёжнее :)
Комментариев нет :
Отправить комментарий