Разбор самых простых задач математической олимпиады Кенгуру для 5-6 класса (задачи 1-6 уровня Ш-2015)
В уровне "Школьник" в Международной математической олимпиаде "Кенгуру" соревнуются ученики 5 и 6 классов. В этом уровне, как в в последующих, участникам даётся уже 30 задач, на выполнение которых выделяется 75 минут. Максимальное количество баллов, которые может набрать участник, равно 30+40+50 = 120.
Давайте начнём разбор решений и ответов с самых простых задач. Многие из них можно предложить и ученикам начальной школы, которые увлекаются математикой.
Задача 1. Половинка (3 балла).
В какой из изображённых в ответах фигур, закрашена ровно половина площади?
Варианты ответа:
А:
; Б: 
; В: 
; Г: 
; Д: 
;
Решение
Легко видеть, что ровно половина площади закрашена в ответе Б. А если время не поджимает, можно в качестве разминки пятикласснику предложить определить, какая часть каждой фигуры закрашена (и попутно вспомнить, что такое дробь).
В ответе А закрашена одна третья часть. В ответе Б - одна вторая, в ответе В - три четверти, в ответе Г - одна четверть. а в ответе Д закрашены две пятые.
Правильный ответ: Б
Задача 2. Зонтик "Кенгуру" (3 балла).
На моём зонтике написано слово KANGAROO, как показано на рисунке. На каком из предложенных в ответах рисунков изображён НЕ мой зонтик?
Варианты ответа:
А:
; Б: 
; В: 
; Г: 
; Д: 
;
Решение
Эта задача почти такая же, как и задача для 3-4 классов, но чуть сложнее. Требуется найти конфигурацию, которой нет на зонтике, а не единственную, которая на нём есть.
Давайте начнём разбор решений и ответов с самых простых задач. Многие из них можно предложить и ученикам начальной школы, которые увлекаются математикой.
Задача 1. Половинка (3 балла).
В какой из изображённых в ответах фигур, закрашена ровно половина площади?
Варианты ответа:
А:
; Б: ; В: ; Г: ; Д: ;Решение
Легко видеть, что ровно половина площади закрашена в ответе Б. А если время не поджимает, можно в качестве разминки пятикласснику предложить определить, какая часть каждой фигуры закрашена (и попутно вспомнить, что такое дробь).
В ответе А закрашена одна третья часть. В ответе Б - одна вторая, в ответе В - три четверти, в ответе Г - одна четверть. а в ответе Д закрашены две пятые.
Правильный ответ: Б
Задача 2. Зонтик "Кенгуру" (3 балла).
На моём зонтике написано слово KANGAROO, как показано на рисунке. На каком из предложенных в ответах рисунков изображён НЕ мой зонтик?Варианты ответа:
А:
; Б: ; В: ; Г: ; Д: ;Решение
Эта задача почти такая же, как и задача для 3-4 классов, но чуть сложнее. Требуется найти конфигурацию, которой нет на зонтике, а не единственную, которая на нём есть.
Найти наименьший положительный корень тригонометрического уравнения
Время от времени я нахожу в математических группах ВКонтакте просьбы о решении школьных математических задач и разбираю их в своём блоге. Вот, например, в одной из контрольных работ самой сложной, 10-й задачей была такая.
Условие
Найти наименьший положительный корень уравнения
1 - sin 2x = (cos 2x + sin 2x)2
Решение
Во-первых, обратим внимание, что во всех тригонометрических функциях аргумент одинаковый и равен 2х. Сделаем замену:
t = 2x
Уравнение превращается в:
1 - sin t = (cos t + sin t)2
Теперь раскроем правую часть, пользуясь формулами сокращённого умножения и тригонометрическими тождествами.
1 - sin t = cos2 t + 2 sin t cos t + sin2 t
1 - sin t = 1 + 2 sin t cos t
- sin t = 2 sin t cos t // вот тут не стоит торопиться сворачивать удвоенное произведение синуса на косинус в синус двойного угла
Условие
Найти наименьший положительный корень уравнения
1 - sin 2x = (cos 2x + sin 2x)2
Решение
Во-первых, обратим внимание, что во всех тригонометрических функциях аргумент одинаковый и равен 2х. Сделаем замену:
t = 2x
Уравнение превращается в:
1 - sin t = (cos t + sin t)2
Теперь раскроем правую часть, пользуясь формулами сокращённого умножения и тригонометрическими тождествами.
1 - sin t = cos2 t + 2 sin t cos t + sin2 t
1 - sin t = 1 + 2 sin t cos t
- sin t = 2 sin t cos t // вот тут не стоит торопиться сворачивать удвоенное произведение синуса на косинус в синус двойного угла
РАсстояния от точки внутри равностороннего треугольника до его сторон
На основной сайт проекта "Приглашение в мир математики" стали заходить, разыскивая решение следующей задачи:
Дан равносторонний треугольник ABC точка D внутри него такая, что расстояние от точки D до сторон треугольника равны 5, 6 и 7 в некотором порядке. Найдите площадь треугольника ABC, SABC.
В решении этой геометрической задачи используется одно интересное свойство правильного трегуольника.
Дело в том, что для любой точки внутри равностороннего трегуольника сумма расстояний от неё до сторон треугольника постоянна и равна высоте этого трегуольника. Для начала докажем это утверджение для точек, лежащих на стороне треугольника.
Дан равносторонний треугольник ABC точка D внутри него такая, что расстояние от точки D до сторон треугольника равны 5, 6 и 7 в некотором порядке. Найдите площадь треугольника ABC, SABC.
В решении этой геометрической задачи используется одно интересное свойство правильного трегуольника.
Дело в том, что для любой точки внутри равностороннего трегуольника сумма расстояний от неё до сторон треугольника постоянна и равна высоте этого трегуольника. Для начала докажем это утверджение для точек, лежащих на стороне треугольника.
Nemters: Numbers from Letters
Google Play: https://play.google.com/store/apps/details?id=air.com.airapport.nemters
AppStore (US): https://apps.apple.com/us/app/nemters/id1473746933
Что будет в сборнике олимпиады "Кенгуру" за 2015-2016 учебный год
Координатор проведения Международного математического конкурса "Кенгуру" Андрей Станиславович Добосевич рассказал о том, какими будут сборники олимпиады по итогам этого учебного года.
Как вы знаете, конкурс проводится в Украине два раза в год. Зимой проходит Всеукраинский этап, в котором участвуют ученики 2-6 классов и решают задачи, ориентированные в основном на логическое мышление. А весной, одновременно в более чем 70 странах мира, проходит Международный этап. В нём участвуют ученики 2-11 классов и решают задачи олимпиадного уровня, соответствующие государственной учебной программе.
Между прочим, обратите внимание: в Международном этапе приглашаются для участия ученики, вне зависимости от их участия во Всеукраинском. Это два независимых конкурса.
Обычно после каждого из конкурсов в школы рассылались сборники задач и решений. Однако в этом году сборник переходит в новый формат. Он будет выпускаться по итогам целого учебного года и будет включать:
Задачи и решения Всеукраинского (зимнего) этапа Кенгуру
Задачи и решения Международного (весеннего) этапа Кенгуру
Задачи и решения с летнего математического лагеря Кенгуру
Задачи, решения и правила Математической карусели, замечательного конкурса по решению задач
Задачи и решения трёх туров заочной математической олимпиады
Задачи и решения очного тура для младшей и старшей лиги
Таким образом информационное наполнение сборника станет намного существеннее. К тому же, переход на новый формат позволит оптимизировать затраты и сумма взноса для участия в олимпиаде "Кенгуру" в следующем году остаётся таким же: 15 гривен.
В каких ещё международных конкурсах можно поучаствовать, потратив 15 гривен? ;) При этом центральный оргкомитет отчитывается о том, как используются эти деньги.
Как вы знаете, конкурс проводится в Украине два раза в год. Зимой проходит Всеукраинский этап, в котором участвуют ученики 2-6 классов и решают задачи, ориентированные в основном на логическое мышление. А весной, одновременно в более чем 70 странах мира, проходит Международный этап. В нём участвуют ученики 2-11 классов и решают задачи олимпиадного уровня, соответствующие государственной учебной программе.
Между прочим, обратите внимание: в Международном этапе приглашаются для участия ученики, вне зависимости от их участия во Всеукраинском. Это два независимых конкурса.
Обычно после каждого из конкурсов в школы рассылались сборники задач и решений. Однако в этом году сборник переходит в новый формат. Он будет выпускаться по итогам целого учебного года и будет включать:
Задачи и решения Всеукраинского (зимнего) этапа Кенгуру
Задачи и решения Международного (весеннего) этапа Кенгуру
Задачи и решения с летнего математического лагеря Кенгуру
Задачи, решения и правила Математической карусели, замечательного конкурса по решению задач
Задачи и решения трёх туров заочной математической олимпиады
Задачи и решения очного тура для младшей и старшей лиги
Таким образом информационное наполнение сборника станет намного существеннее. К тому же, переход на новый формат позволит оптимизировать затраты и сумма взноса для участия в олимпиаде "Кенгуру" в следующем году остаётся таким же: 15 гривен.
В каких ещё международных конкурсах можно поучаствовать, потратив 15 гривен? ;) При этом центральный оргкомитет отчитывается о том, как используются эти деньги.
Олимпиада Кенгуру-2016 в Кировограде
Уважаемые координаторы школ!
За заданиями олимпиады, бланками ответов и прочими материалами, обращайтесь, пожалуйста, после 9 марта по адресу:
Школа №17, ул.Комарова, 54.
Сорока Светлана Николаевна
Телефон: 050-45-75-099
Чему равен синус тридцати пяти градусов
На вопрос, чему равен синус тридцати пяти градусов:
- Математик ответил, что синус тридцати пяти градусов не выражается алгебраическим числом.
- Инженер прикинул: синус тридцати равен одной второй, синус сорока пяти равен корню из двух на два, это примерно ноль целых семь десятых, значит, интерполировав, синус тридцати пяти будет равен примерно пятьдесят семь сотых.
- Физик достал калькулятор, нажал кнопки DEG - 3 - 5 - sin, результат округлил до тысячных и получил 0.574.
- Школьник на контрольной работе по решению треугольников достал четырёхзначные таблицы Брадиса, порадовался, что угол дан в целых градусах и не нужно брать поправку на минуты и секунды, и нашёл в таблице результат: 0,5726
- Программист написал функцию, вычисляющую синус как сумму ряда Тейлора: $35-\frac{35^3}{3!}+\frac{35^5}{5!}-\frac{35^7}{7!}+\frac{35^9}{9!}-\dots$, но упёрся в пороговое значение double. "А, так аргумент ведь в радианах брать надо было!" - догадался он, и пообещал исправить ошибку в следующей версии.
- Математик-тролль ответил, что синус тридцати пяти градусов в точности равен косинусу пятидесяти пяти градусов.
- Юный любитель математики и будущий обладатель медали Филдса, задумав расширить табличку синусов, которую старший брат как раз изучал на уроках алгебры, построил с помощью транспортира угол в 35 градусов, достроил его до прямоугольного треугольника, измерил противолежащий катет и гипотенузу и нашёл их отношение: $\frac{39}{68}$.
- А на лекциях такого не было! - применил своё стандартное заклинание студент-первокурсник.
- Синус тридцати пяти градусов равняется, как вычислить sin 35, ышт 35 градусов посчитать, синус, косинус, математика, решение, 9 класс, скачать учебник гдз ответы на ЗНО и ЕГЭ 2016 без регистрации и смс, - написал СЕОшник.
Это была присказка. Перейдём теперь к непосредственному изложению сути этого поста.
Сборники олимпиады Кенгуру-2015 рассылаются по школам
Также каждый участник получит полезный сувенир, о котром мы писали ранее.
Просьба координаторам школ срочно связаться с региональным координатором и забрать материалы.
Превращаем цифры в забавных животных - занятие для будущих первоклассников и их родителей
Давайте чуть-чуть отвлечёмся от математики и вспомним, что ещё лето. Вот какие забавные рисунки попались в одноклассниках. Берём цифры или числа и превращаем их в рисунки! Отличное занятие для того, чтобы провести время с будущими первоклассниками!
Из числа 29 получился лебедь:
Акула из двух двоек:
Кстати, вот как из двух двоек получить пятёрку, пользуясь тригонометрическими функциями
Из числа 29 получился лебедь:
Цапля из одной двойки:
Как Ричард Фейнман победил японского вычислителя
В книге нобелевского лауреата Ричарда Фейнмана "Вы, конечно же, шутите, мистер Фейнман", описывается интересное математическое состязание. Приводим его с нашими математическими комментариями по переводу книги из Библиотеки Мошкова.
Первое время, когда я приехал в Бразилию, я не знал, в какое время там принято обедать. Я приходил в рестораны, когда там никого не было, заказывал рис со стейком (который очень любил), а четыре официанта стояли вокруг.
Как-то в ресторан зашел японец. Я видел его раньше, он бродил поблизости, пытаясь продавать счеты. Он заговорил с официантами и бросил им вызов, сказав, что может складывать числа быстрее, чем кто-либо другой. Они не очень-то хотели терять лицо и сказали: "Да, конечно. Почему бы тебе ни поспорить вон с тем посетителем?"
Он подошел ко мне, но я запротестовал: "Но я не достаточно хорошо говорю по-португальски!"
Официанты засмеялись и сказали: "Числа - это просто".
Они принесли мне карандаш и бумагу.
Первое время, когда я приехал в Бразилию, я не знал, в какое время там принято обедать. Я приходил в рестораны, когда там никого не было, заказывал рис со стейком (который очень любил), а четыре официанта стояли вокруг.
Как-то в ресторан зашел японец. Я видел его раньше, он бродил поблизости, пытаясь продавать счеты. Он заговорил с официантами и бросил им вызов, сказав, что может складывать числа быстрее, чем кто-либо другой. Они не очень-то хотели терять лицо и сказали: "Да, конечно. Почему бы тебе ни поспорить вон с тем посетителем?"
Он подошел ко мне, но я запротестовал: "Но я не достаточно хорошо говорю по-португальски!"
Официанты засмеялись и сказали: "Числа - это просто".
Они принесли мне карандаш и бумагу.
Синусы каких углов выражаются формулами?
В 8 классе ученики заучивают таблицу синусов и других тригонометрических функций. Она выглядит так:
Есть очень хороший мнемонический приём, позволяющий запомнить значения тригонометрических функций табличных углов. Однако составители ЗНО, видимо, считают, что держать эти числа в голове не стоит, потому как всегда помещают тригонометрическую таблицу на обложку тетрадей с задачами тестирования.
Нерадивые ученики наличием такой таблицы объясняют своё нежелание заучивать формулы. Но у интересующихся математикой закономерно возникает другой вопрос - а выражаются ли с помощью формул с корнями синусы других целых углов?
угол $\alpha$, o
|
0
|
30
|
45
|
60
|
90
|
sin$\alpha$
|
0
|
$\frac{1}{2}$
|
$\frac{\sqrt{2}}{2}$
|
$\frac{\sqrt{3}}{2}$
|
1
|
cos$\alpha$
|
1
|
$\frac{\sqrt{3}}{2}$
|
$\frac{\sqrt{2}}{2}$
|
$\frac{1}{2}$
|
0
|
tg$\alpha$
|
0
|
$\frac{1}{\sqrt{3}}$
|
1
|
$\sqrt{3}$
|
-
|
ctg$\alpha$
|
-
|
$\sqrt{3}$
|
1
|
$\frac{1}{\sqrt{3}}$
|
0
|
Есть очень хороший мнемонический приём, позволяющий запомнить значения тригонометрических функций табличных углов. Однако составители ЗНО, видимо, считают, что держать эти числа в голове не стоит, потому как всегда помещают тригонометрическую таблицу на обложку тетрадей с задачами тестирования.
Нерадивые ученики наличием такой таблицы объясняют своё нежелание заучивать формулы. Но у интересующихся математикой закономерно возникает другой вопрос - а выражаются ли с помощью формул с корнями синусы других целых углов?
У кого шансы вытащить жребий больше: у первого или остальных
Часто в ситуациях, когда нужно тянуть жребий, участники оспаривают друг у друга порядок его вытягивания. Они полагают, что от порядка зависит вероятность успеха или неудачи. Покажем, что это не так. Для примера можно рассматривать вытягивание одной короткой спички среди 5 длинных или самый экстремальный случай - игру в русскую рулетку. Но вдохновила на написание этого поста задача, предложенная участником группы "Типичный математик" в VK. Её и разберём.
Задача по теории вероятности
Есть 10 карт, из них 7 красных и 3 черных. Их раздают десяти игрокам по очереди (каждому по одной). Верно ли, что при большом количестве экспериментов, вероятность выпадения первому игроку черных карт больше, чем остальным?
Решение
Задача по теории вероятности
Есть 10 карт, из них 7 красных и 3 черных. Их раздают десяти игрокам по очереди (каждому по одной). Верно ли, что при большом количестве экспериментов, вероятность выпадения первому игроку черных карт больше, чем остальным?
Решение
Разбор задач 19-24 для 3-4 классов олимпиады Кенгуру по математике (решения и ответы на самые сложные задачи уровня М34-2015)
Завершаем разбор решений и ответов на задачи конкурса Кенгуру для 3 и 4 классов. Здесь 6 самых сложных задач, в которых используется комбинаторика, делимость, конструкции и логические рассуждения.
Задача 19. Извилистый берег (5 баллов).
На рисунке - остров, на котором растёт пальма и сидят несколько лягушек. Остров ограничен береговой линией. Сколько лягушек сидят НА ОСТРОВЕ?
Варианты ответа:
А: 5; Б: 6; В: 7; Г: 8; Д: 10;
Решение
При решении этой задачи на компьютере можно использовать инструмент "Заливка". Теперь наглядно видно, что на острове сидят 6 лягушек.
Сделать что-то подобное этой заливке можно было и карандашом на листочке условий. Но есть ещё один интересный способ, позволяющий определить, находится ли точка внутри замкнутой несамопересекающейся кривой или снаружи.
Соединим эту точку (лягушку) с точкой, о которой мы точно знаем, что она находится снаружи кривой. Если соединяющая линия будет иметь нечётное количество пересечений с кривой, то наша точка лежит внутри (т.е. на острове), а если чётное - то снаружи (на воде)
Правильный ответ: Б 6
Задача 20. Числа на мячах (5 баллов).
У Мудрагелика 10 мячей, пронумерованных от 0 до 9. Он разделил эти мячи между тремя своими друзьями. Ласунчик получил три мяча, Красунчик - четыре, Сонько - три. Потом Мудрагелик попросил каждого их своих друзей перемножить числа на полученных мячах. Ласунчик получил произведение, равное 0, Красунчик - 72, а Сонько - 90. Все кенгурята правильно перемножили числа. Чему равна сумма чисел на тех мячах, которые получил Ласунчик?
Варианты ответа:
А: 11; Б: 12; В: 13; Г: 14; Д: 15;
Задача 19. Извилистый берег (5 баллов).
На рисунке - остров, на котором растёт пальма и сидят несколько лягушек. Остров ограничен береговой линией. Сколько лягушек сидят НА ОСТРОВЕ?
Варианты ответа:
А: 5; Б: 6; В: 7; Г: 8; Д: 10;
Решение
При решении этой задачи на компьютере можно использовать инструмент "Заливка". Теперь наглядно видно, что на острове сидят 6 лягушек.
Сделать что-то подобное этой заливке можно было и карандашом на листочке условий. Но есть ещё один интересный способ, позволяющий определить, находится ли точка внутри замкнутой несамопересекающейся кривой или снаружи.Соединим эту точку (лягушку) с точкой, о которой мы точно знаем, что она находится снаружи кривой. Если соединяющая линия будет иметь нечётное количество пересечений с кривой, то наша точка лежит внутри (т.е. на острове), а если чётное - то снаружи (на воде)
Правильный ответ: Б 6
Задача 20. Числа на мячах (5 баллов).
У Мудрагелика 10 мячей, пронумерованных от 0 до 9. Он разделил эти мячи между тремя своими друзьями. Ласунчик получил три мяча, Красунчик - четыре, Сонько - три. Потом Мудрагелик попросил каждого их своих друзей перемножить числа на полученных мячах. Ласунчик получил произведение, равное 0, Красунчик - 72, а Сонько - 90. Все кенгурята правильно перемножили числа. Чему равна сумма чисел на тех мячах, которые получил Ласунчик?
Варианты ответа:
А: 11; Б: 12; В: 13; Г: 14; Д: 15;
Разбор задач 13-18 для 3 и 4 классов математической олимпиады Кенгуру (уровень М3-4 2015)
Задача 13. Расставь игрушки (4 балла).
У Красунчика 4 игрушки: автомобиль, кукла, мяч и кораблик. Он хочет поставить их в ряд на полку. Автомобиль должен быть рядом с кораблём, а кукла - рядом с автомобилем. Сколькими способами он может расставить их так, чтобы эти условия выполнялись?
Варианты ответа:
А: 2-мя; Б: 4-мя; В: 5-ю; Г: 6-ю; Д: 8-ю;
Решение
Вот и задача на комбинаторику в 3 классе! В расположении игрушек в условии даны две жёсткие пары: (Автомобиль - Корабль) и (Кукла - Автомобиль). Приглядевшись, понимаем, что эти две пары на самом деле тройка: (Кукла - Автомобиль - Корабль). Эти три игрушки должны стоять на полке рядом. Причём стоять они могут как в таком порядке, так и в обратном: (Корабль - Автомобиль - Кукла).
Оставшаяся игрушка, Мяч, может стоять как слева от этой тройки, так и справа. Всего получается 4 способа:
1. Мяч - Кукла - Автомобиль - Корабль
2. Кукла - Автомобиль - Корабль - Мяч
3. Мяч - Корабль - Автомобиль - Кукла
4. Корабль - Автомобиль - Кукла - Мяч
Правильный ответ: Б 4-мя способами
Задача 14. Велосипедная прогулка по парку (4 балла).
Петя ездит на велосипеде по парку (схема парка - на рисунке). Свой маршрут он начинает с точки S и движется в направлении стрелки. На первом перекрёстке мальчик поворачивает направо, на втором - налево, потом снова направо, затем - опять налево, и так далее, в таком же порядке. Через какой перекрёсток НЕ будет проезжать Петя?
У Красунчика 4 игрушки: автомобиль, кукла, мяч и кораблик. Он хочет поставить их в ряд на полку. Автомобиль должен быть рядом с кораблём, а кукла - рядом с автомобилем. Сколькими способами он может расставить их так, чтобы эти условия выполнялись?
Варианты ответа:
А: 2-мя; Б: 4-мя; В: 5-ю; Г: 6-ю; Д: 8-ю;
Решение
Вот и задача на комбинаторику в 3 классе! В расположении игрушек в условии даны две жёсткие пары: (Автомобиль - Корабль) и (Кукла - Автомобиль). Приглядевшись, понимаем, что эти две пары на самом деле тройка: (Кукла - Автомобиль - Корабль). Эти три игрушки должны стоять на полке рядом. Причём стоять они могут как в таком порядке, так и в обратном: (Корабль - Автомобиль - Кукла).
Оставшаяся игрушка, Мяч, может стоять как слева от этой тройки, так и справа. Всего получается 4 способа:
1. Мяч - Кукла - Автомобиль - Корабль
2. Кукла - Автомобиль - Корабль - Мяч
3. Мяч - Корабль - Автомобиль - Кукла
4. Корабль - Автомобиль - Кукла - Мяч
Правильный ответ: Б 4-мя способами
Задача 14. Велосипедная прогулка по парку (4 балла).
Петя ездит на велосипеде по парку (схема парка - на рисунке). Свой маршрут он начинает с точки S и движется в направлении стрелки. На первом перекрёстке мальчик поворачивает направо, на втором - налево, потом снова направо, затем - опять налево, и так далее, в таком же порядке. Через какой перекрёсток НЕ будет проезжать Петя?Разбор задач 7-12 для 3 и 4 классов математической олимпиады Кенгуру(уровень М3-4 2015)
В этом выпуске мы завершим разбор простых задач математической олимпиады "Кенгуру-2015" для 3 и 4 классов и перейдём к средним.
Задача 7. Карточки с картинками (3 балла).
У Красунчика есть 5 карточек, вот они:
Есть карточки, на которых с одной стороны нарисован цветок, а с другой - собака. А есть такие, на которых с одной стороны нарисована кошка, а с другой - дерево. Сколько карточек с цветочками у Красунчика?
Варианты ответа:
А: 1; Б: 2; В: 3; Г: 4; Д: 5;
Решение
Из условия понятно, что на карточках рисунки с двух сторон. Нам надо определить, какие рисунки на тех сторонах, которые не видны. Так как "одна" и "другая" стороны карточки равноценны, то утверждения из условия работают в обе стороны. Выходит, на первой карточке под деревом нарисована кошка. На второй под собакой - цветок. На третьей под кошкой - дерево. На четвёртой карточке снова под собакой нарисован цветок. И на пятой под цветком нарисована собака. Выходит, всего карточек с цветками три: вторая, четвёртая и пятая.
Кстати, двусторонние карточки используются в одной классической задаче на математическую логику, о которой мы как-нибудь расскажем в разделе Занимательной математики.
Правильный ответ: В 3
Задача 8. Зонтик "Кенгуру" (3 балла).
На моём зонтике написано слово KANGAROO, как показано на рисунке. На каком из предложенных в ответах рисунков тоже изображён мой зонтик?
Эта задача проходит через несколько классов и использовалась для мониторинга уровня учеников.
Варианты ответа:
А:
; Б: 
; В: 
; Г: 
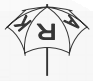; Д: 
;
Решение
Задача 7. Карточки с картинками (3 балла).
У Красунчика есть 5 карточек, вот они:
Есть карточки, на которых с одной стороны нарисован цветок, а с другой - собака. А есть такие, на которых с одной стороны нарисована кошка, а с другой - дерево. Сколько карточек с цветочками у Красунчика?
Варианты ответа:
А: 1; Б: 2; В: 3; Г: 4; Д: 5;
Решение
Из условия понятно, что на карточках рисунки с двух сторон. Нам надо определить, какие рисунки на тех сторонах, которые не видны. Так как "одна" и "другая" стороны карточки равноценны, то утверждения из условия работают в обе стороны. Выходит, на первой карточке под деревом нарисована кошка. На второй под собакой - цветок. На третьей под кошкой - дерево. На четвёртой карточке снова под собакой нарисован цветок. И на пятой под цветком нарисована собака. Выходит, всего карточек с цветками три: вторая, четвёртая и пятая.
Кстати, двусторонние карточки используются в одной классической задаче на математическую логику, о которой мы как-нибудь расскажем в разделе Занимательной математики.
Правильный ответ: В 3
Задача 8. Зонтик "Кенгуру" (3 балла).
На моём зонтике написано слово KANGAROO, как показано на рисунке. На каком из предложенных в ответах рисунков тоже изображён мой зонтик?Эта задача проходит через несколько классов и использовалась для мониторинга уровня учеников.
Варианты ответа:
А:
; Б: ; В: ; Г: ; Д: ;Решение
Как решать задачу на проценты, определить процент отходов по массам нетто-брутто
Видимо, будущие шестиклассники готовятся к школе, решая задачи наперёд, или повторяют математику за пятый класс. Сегодня на "ответах" появился ряд просьб о помощи с похожими заданиями.
Приведём одну из них и покажем детально по шагам, как они решаются.
Приведём одну из них и покажем детально по шагам, как они решаются.
Задача на проценты
Для приготовления фреша было взято 3 килограмма апельсина (брутто). После ручной обработки мы получили 2.10 кг (нетто). Определите процент отходов.Решение задачи на проценты
Задачи на проценты решаются почти так же, как и задачи на дроби. Просто стоит помнить, что один процент - это дробь одна сотая (отсюда и пошло название и символ процента).Разбор задач 1-6 для 3 и 4 классов математической олимпиады Кенгуру(уровень М3-4 2015)
Разберём задачи олимпиады Кенгуру по математике для 3 и 4 класса. В уровне Малыш 3-4 ученикам даётся 24 задачи, по 8 на каждый уровень сложности. На решение задач выделяется 75 минут. Максимальное количество баллов, которое может набрать участник, правильно решивший все задачи - 96.
В 3 и 4 классах в задачах уже появляются элементы комбинаторики, математические ребусы, разрезания и классические рыцари и лжецы.
Задача 1. Цепочка вычислений (3 балла).
Какое число окажется в синем облачке, если все действия выполнить верно?
Варианты ответа:
А: 6; Б: 7; В: 8; Г: 10; Д: 15;
Решение
В 3 и 4 классах в задачах уже появляются элементы комбинаторики, математические ребусы, разрезания и классические рыцари и лжецы.
Задача 1. Цепочка вычислений (3 балла).
Какое число окажется в синем облачке, если все действия выполнить верно?
Варианты ответа:
А: 6; Б: 7; В: 8; Г: 10; Д: 15;
Решение
Подписаться на:
Сообщения
(
Atom
)